Нормальное распределение вероятность что случайная величина примет значение больше

Нормальное распределение вероятность что случайная величина примет значение больше

Тема «Нормальное распределение»

Нормальным называют распределение вероятностей непрерывной случайной величины, которое задается плотностью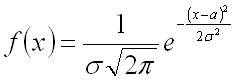
.
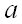
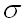
Нормальное распределение задается двумя параметрами: – математическим ожиданием, – средним квадратическим отклонением.
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
Нормированным называют нормальное распределение с параметрами .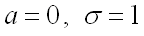
Плотность нормированного распределения задается формулой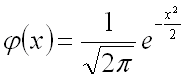
.

Вероятность попадания в заданный интервал нормальной случайной величины

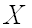
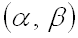
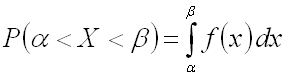
Как уже было установлено, вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , равна определенному интегралу от плотности распределения, взятому в соответствующих пределах:
.
Для нормально распределенной случайной величины соответственно получим: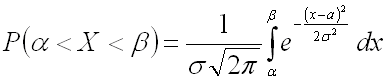
.
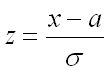
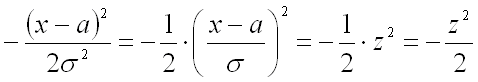
Преобразуем последнее выражение, введя новую переменную . Следовательно, показатель степени выражения, стоящего под интегралом преобразуется в:
.
Для замены переменной в определенном интеграле еще необходимо заменить дифференциал и пределы интегрирования, предварительно выразив переменную из формулы замены: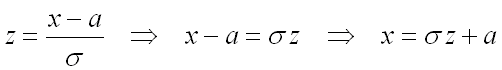
;
;
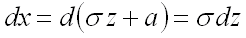
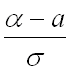
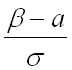
– нижний предел интегрирования;
– верхний предел интегрирования;
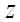
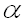
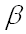
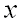
(для нахождения пределов интегрирования по новой переменной в формулу замены переменной были подставлены и – пределы интегрирования по старой переменной ).
Подставим все в последнюю из формул для нахождения вероятности: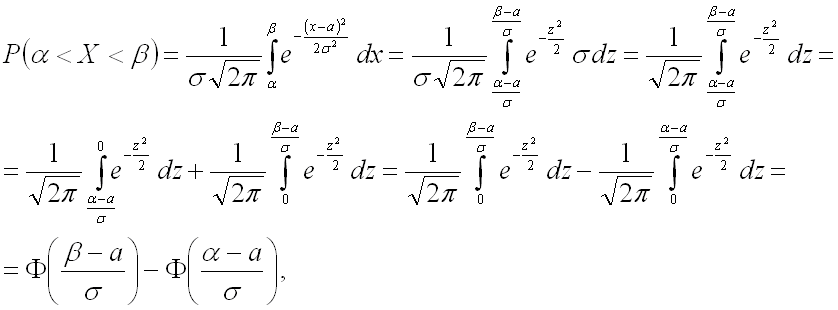

где 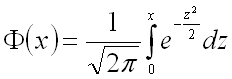– функция Лапласа.
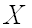
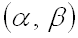
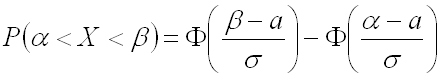
Вывод: вероятность того, что нормально распределенная случайная величина примет значение, принадлежащее интервалу , равна:
,
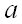
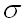
где – математическое ожидание, – среднее квадратическое отклонение данной случайной величины.

Примеры решения задач

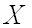
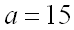
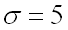
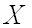
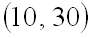
Пример 1. Случайная величина имеет нормальное распределение с математическим ожиданием и средним квадратическим отклонением . Найти вероятность того, что случайная величина примет значение, принадлежащее интервалу .

Решение.

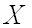
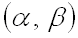
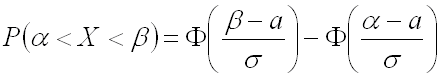
Известно, что вероятность того, что нормально распределенная случайная величина примет значение, принадлежащее интервалу , равна:
,
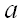
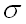
где – математическое ожидание, – среднее квадратическое отклонение.
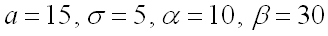
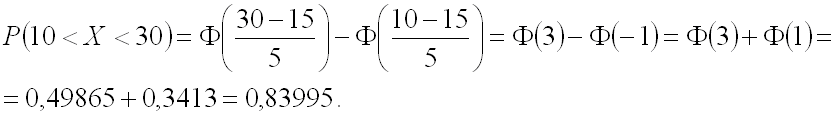
По условию . Следовательно,

Ответ: .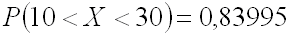

Вычисление вероятности заданного отклонения

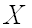
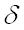
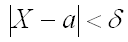
Вычислим вероятность того, что отклонение нормально распределенной случайной величины от своего математического ожидания по абсолютной величине не превысит , то есть вероятность осуществления неравенства .
Заменим неравенство с модулем равносильным ему двойным неравенством: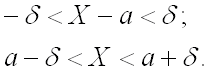

Теперь мы можем воспользоваться формулой для нахождения вероятности попадания в заданный интервал нормальной случайной величины, где границами интервала являются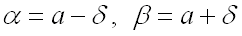
:

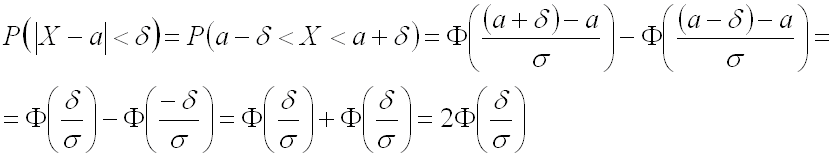
(в последних преобразованиях использовано свойство нечетности функции Лапласа: ).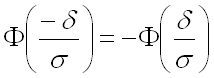
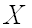
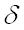
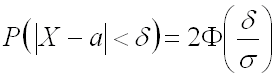
Вывод: вероятность того, что отклонение нормально распределенной случайной величины от своего математического ожидания по абсолютной величине не превысит , равна:
,
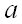
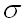
где – математическое ожидание, – среднее квадратическое отклонение.

Примеры решения задач

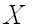
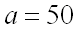
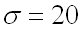
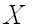
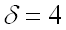
Пример 1. Случайная величина имеет нормальное распределение с математическим ожиданием и средним квадратическим отклонением . Найти вероятность того, что случайная величина отклонится от своего математического ожидания по абсолютной величине не больше, чем на .

Решение.

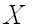
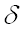
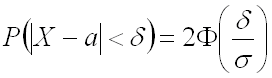
Известно, что вероятность того, что отклонение нормально распределенной случайной величины от своего математического ожидания по абсолютной величине не превысит , равна:
,
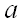
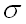
где – математическое ожидание, – среднее квадратическое отклонение.
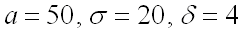
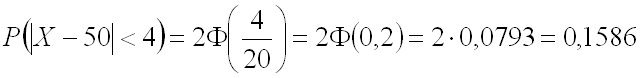
По условию . Следовательно,
.

Ответ: .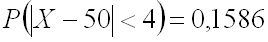

Правило трех сигм

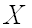
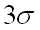
Вычислим вероятность того, что отклонение нормально распределенной случайной величины от своего математического ожидания по абсолютной величине не превысит .
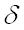
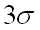
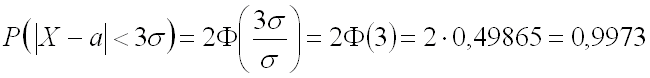
Воспользуемся формулой для нахождения вероятности заданного отклонения, в которую в качестве подставим :
.
Таким образом, вероятность того, что отклонение случайной величины 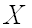по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.
Другими словами, вероятность того, что абсолютная величина отклонения превысит 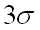, составляет всего 0,0027. Такое событие, исходя их принципа невозможности маловероятных событий, можно считать практически невозможным.
Вывод (правило трех сигм): если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

Понятие о теореме Ляпунова

Известно, что нормально распределенные случайные величины широко распределены на практике. Объяснение этому было дано А.М.Ляпуновым в центральной предельной теореме: если случайная величина 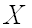представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному.

Источник

Нормальное распределение непрерывной случайной величины

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Нормальное распределение: теория и практика

Вероятность встретить в выборке те или иные значение равна площади фигуры под кривой и в случае нормального распределения мы видим, что под верхом «колокола», которому соответствуют значения, стремящиеся к среднему, площадь, а значит, вероятность, больше, чем под краями. Таким образом, получаем то же, что уже сказано: вероятность встретить человека «нормального» роста, поймать рыбу «нормальной» массы выше, чем для значений, отличающихся в бОльшую или меньшую сторону. В очень многих случаях практики ошибки измерения распределяются по закону, близкому к нормальному.

Если копнуть глубже, то нормальное распределение можно найти в распределении многих показателях в системах связи (сигналы, шумы, помехи и другие), под нормальное распределение подгоняют многие финансовые показатели. Хотя следует подчеркнуть, что именно подгоняют, поскольку признаки нормальности в этих случаях часто бывают смещены.

Остановимся ещё раз на рисунке в начале урока, на котором представлена функция плотности нормального распределения. График этой функции получен при рассчёте некоторой выборки данных в пакете программных средств STATISTICA. На ней столбцы гистограммы представляют собой интервалы значений выборки, распределение которых близко (или, как принято говорить в статистике, незначимо отличаются от) к собственно графику функции плотности нормального распределения, который представляет собой кривую красного цвета. На графике видно, что эта кривая действительно колоколообразная.

Нормальное распределение во многом ценно благодаря тому, что зная только математическое ожидание непрерывной случайной величины и стандартное отклонение, можно вычислить любую вероятность, связанную с этой величиной.

Что влияет на график плотности нормального распределения

Чуть далее мы разберем довольно ужасную на первый взгляд формулу функции плотности нормального распределения. А пока остановимся на важнейших параметрах, связанных с этой формулой, которые влияют на вид графика плотности нормального распределения.

Коэффициент асимметрии (β 1 ). Если он равен нулю, то график плотности нормального распределения симметричен относительно среднего. Если он отличен от нуля, то распределение случайной величины несимметрично, причем, если коэффициент положителен, то правый хвост длиннее, а если отрицателен, то длиннее левый хвост. Это показано на графике снизу.

Коэффициент эксцесса (β 2 ). Характеризует остроту вершины графика плотности нормального распределения. Чем больше значение коэффициента, тем острее вершина. Это показано на графике снизу.

Подробнее о функции плотности нормального распределения

Функцию плотности нормального распределения непрерывной случайной величины можно найти по формуле:

,

Свойства функции плотности нормального распределения

Повторим знания о графиках функции плотности. Изменения среднего значения перемещают кривую функции плотности нормального распределения в направлении оси Ox. Если возрастает, кривая перемещается вправо, если уменьшается, то влево.

Вероятность попадания значения нормально распределённой случайной величины в заданный интервал

Интегральная функция нормального распределения:

.

Однако проблематично получить таблицы для каждой возможной комбинации среднего и стандартного отклонения. Поэтому одним из простых способов вычисления вероятности попадания нормально распределённой случайной величины в заданный интервал является использование таблиц вероятностей для стандартизированного нормального распределения.

Стандартизованным или нормированным называется нормальное распределение, среднее значение которого , а стандартное отклонение .

Функция плотности стандартизованного нормального распределения:

.

Интегральная функция стандартизованного нормального распределения:

.

На рисунке ниже представлена интегральная функция стандартизованного нормального распределения, график которой получен при рассчёте некоторой выборки данных в пакете программных средств STATISTICA. Собственно график представляет собой кривую красного цвета, а значения выборки приближаются к нему.

Для увеличения рисунка можно щёлкнуть по нему левой кнопкой мыши.

Стандартизация случайной величины означает переход от первоначальных единиц, используемых в задании, к стандартизованным единицам. Стандартизация выполняется по формуле

.

На практике все возможные значения случайной величины часто не известны, поэтому значения среднего и стандартного отклонения точно определить нельзя. Их заменяют средним арифметическим наблюдений и стандартным отклонением s. Величина z выражает отклонения значений случайной величины от среднего арифметического при измерении стандартных отклонений.

Открытый интервал

Таблица вероятностей для стандартизированного нормального распределения, которая есть практически в любой книге по статистике, содержит вероятности того, что имеющая стандартное нормальное распределение случайная величина Z примет значение меньше некоторого числа z. То есть попадёт в открытый интервал от минус бесконечности до z. Например, вероятность того, что величина Z меньше 1,5, равна 0,93319.

Пример 1. Предприятие производит детали, срок службы которых нормально распределён со средним значением 1000 и стандартным отклонением 200 часов.

Для случайно отобранной детали вычислить вероятность того, что её срок службы будет не менее 900 часов.

Решение. Введём первое обозначение:

— искомая вероятность.

Значения случайной величины находятся в открытом интервале. Но мы умеем вычислять вероятность того, что случайная величина примет значение, меньшее заданного, а по условию задачи требуется найти равное или большее заданного. Это другая часть пространства под кривой плотности нормального распределения (колокола). Поэтому, чтобы найти искомую вероятность, нужно из единицы вычесть упомянутую вероятность того, что случайная величина примет значение, меньше заданного 900:

Теперь случайную величину нужно стандартизировать.

Продолжаем вводить обозначения:

По этим данным условия задачи получаем:

.

По таблицам стандартизированной случайной величине (границе интервала) z = −0,5 соответствует вероятность 0,30854. Вычтем ее из единицы и получим то, что требуется в условии задачи:

.

Итак, вероятность того, что срок службы детали будет не менее 900 часов, составляет 69%.

Пример 2. В некотором городе среднегодовой доход семьи является нормально распределённой случайной величиной со средним значением 300000 и стандартным отклонением 50000. Известно, что доходы 40 % семей меньше величины A. Найти величину A.

Чтобы найти величину A, сначала составим интегральную функцию:

.

Поэтому составляем равенство

и находим его решение:

Ответ: доходы 40 % семей менее 287300.

Закрытый интервал

Подсказка: в этой задаче помимо нахождения вероятности попадания случайной величины в закрытый интервал (вероятность получения небракованной детали) требуется выполнить ещё одно действие.

Приближенный метод проверки нормальности распределения

Приближенный метод проверки нормальности распределения значений выборки основан на следующем свойстве нормального распределения: коэффициент асимметрии β 1 и коэффициент эксцесса β 2 равны нулю.

Коэффициент асимметрии β 1 численно характеризует симметрию эмпирического распределения относительно среднего. Если коэффициент асимметрии равен нулю, то среднее арифметрического значение, медиана и мода равны: и кривая плотности распределения симметрична относительно среднего. Если коэффициент асимметрии меньше нуля ( β 1 ), то среднее арифметическое меньше медианы, а медиана, в свою очередь, меньше моды () и кривая сдвинута вправо (по сравнению с нормальным распределением). Если коэффициент асимметрии больше нуля ( β 1 > 0 ), то среднее арифметическое больше медианы, а медиана, в свою очередь, больше моды () и кривая сдвинута влево (по сравнению с нормальным распределением).

Коэффициент эксцесса β 2 характеризует концентрацию эмпирического распределения вокруг арифметического среднего в направлении оси Oy и степень островершинности кривой плотности распределения. Если коэффициент эксцесса больше нуля, то кривая более вытянута (по сравнению с нормальным распределением) вдоль оси Oy (график более островершинный). Если коэффициент эксцесса меньше нуля, то кривая более сплющена (по сравнению с нормальным распределением) вдоль оси Oy (график более туповершинный).

Коэффициент асимметрии можно вычислить с помощью функции MS Excel СКОС. Если вы проверяете один массив данных, то требуется ввести диапазон данных в одно окошко «Число».

Коэффициент эксцесса можно вычислить с помощью функции MS Excel ЭКСЦЕСС. При проверке одного массива данных также достаточно ввести диапазон данных в одно окошко «Число».

Для коэффициента асимметрии β 1 :

,

— квантиль стандартного нормального распределения уровня ,

Для коэффициента эксцесса β 2 :

,

— квантиль стандартного нормального распределения уровня ,

Нормальное распределение и расчёты в MS Excel

Значения функции плотности f(x) и интегральной функции F(x) нормального распределения можно вычислить при помощи функции MS Excel НОРМ.РАСП. Окно для соответствующего расчёта показано ниже (для увеличения нажать левой кнопкой мыши).

MS Excel требует ввести следующие данные:

Решим ещё задачи на нормальное распределение

Решить задачу самостоятельно, а затем посмотреть решение

Решим ещё одну задачу вместе

Пример 6. О случайной величине X известно, что она нормально распределена, а вероятности того, что она составит 10 или меньше и больше 25, соответственно и . Найти среднее значение (математическое ожидание) случайной величины и её дисперсию.

Решение. Используем данные в условии задачи вероятности:

Пользуясь статистическими таблицами, находим:

Составляем систему из полученных равенств:

Решая систему, находим:

.

Источник